# Data Matrices and Linear Transformation ### Data and Linear Regression See [Data and Linear Regression](Data%20and%20Linear%20Regression.md). ### Data and linear transformations See this fantastic post [Singular Value Decomposition Part 1: Perspectives on Linear Algebra – Math ∩ Programming](https://jeremykun.com/2016/04/18/singular-value-decomposition-part-1-perspectives-on-linear-algebra/). ### Archive Generally I interpret matrices to represent linear transformations. However, there a few cases where this mental model seems to struggle: 1. When the matrix is a "data matrix". For instance, it has $n$ observations (rows) and $d$ columns (dimensions). Can this actually be thought of in any capacity as a linear transformation? I don't think so. This is really just a subset of our vector space, with associated labels. It is simply easy to store this way. 2. 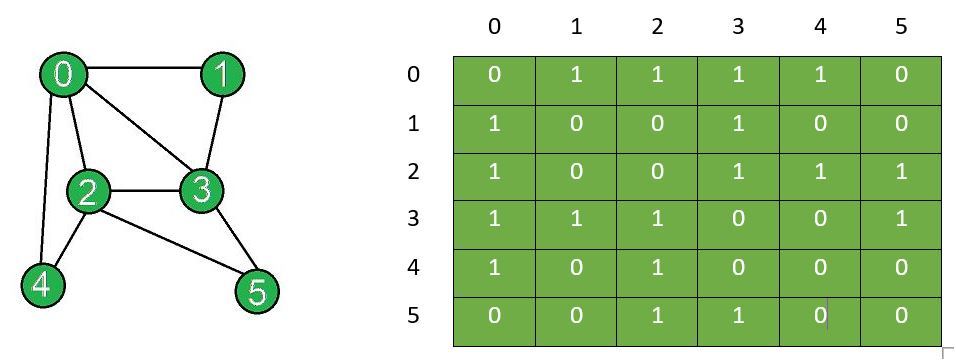When the matrix is an adjacency matrix:  3. When the data is a *similarity matrix* or a distance matrix (pairwise distance between all $n$ points, so matrix is $n \times n$) ### Notes * Look at columns as noting where the basis lands in our new space (whatever that space is) * Linear transformation on space of adjacencys * Part of power of adjacency matrix is ability to exponentiate * Not a vector space, instead it is a module (may be...) * vector spaces are defined over fields * Adjacency will always contain natural numbers * Integer valued ? * Module over $\mathbb{Z}$ * Ring is field where you can't necessarily divide * Z is a ring, but not a field * This has implications for matrices over Z * Adjacency matrix can be used as a data structure * Answer: * They are not linear transformations! * It is not clear what adding those things would be. It needs to for this to be a linear transformation * New Answer: * they may be! * This is basis for space of paths? * may be operating on space of paths? ### Random notes My fundamental question is how to think of a linear transformation when it was based on a similarity Data matrix what do eigenvalues mean in this context Is this a transformation? Of what? It may literally be a transformation from d to n dimensions! Each point (n original) now has its own “dimension” where we see how close it is to all other points! We then wish to find the eigenvextors of this matrix since they represent a fundamental structure of the matrix Question: how is this a linear transformation? How di basis vectors play a role? Orthogonality?