# Galton Board The following is taken from [here](https://youtu.be/gm7VDk8kxOw?list=PLrxfgDEc2NxY_fRExpDXr87tzRbPCaA5x&t=527). > What is encoded and where? Consider the bell curve that arises when dropping marbles in a Galton board. Where does the shape of that curve arise from? In a certain sense (at a micro level) you could potentially calculate it out and predict it, but in a larger sense that shape is *not* encoded anywhere in the material of the marbles or the definition of the board. That device is harnessing particular laws of physics. 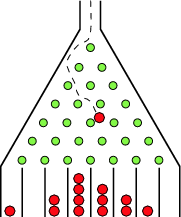### A Note on Galton Boards  The question arises, *what makes a Galton board work?* In a sense, the answer is dual pronged: 1. This is a physical configuration that embodies a binomial distribution. In other words, the "generating process" under the hood is the binomial distribution. 2. The second part (a key part), is *why* does this board converge to what is expected from a binomial distribution? The answer lies in the fact that physical configuration ensures that at each successive depth level there is a 50% chance of the ball bouncing to the left or right. This is combined with the fact that at any given step the ball can *only* move to the right or left a single step; it *cannot* move 2, 3, 4, or 9 steps to the right or left-only one. We also have the fact that a ball will fall downwards due to gravity, and other similar constraints as such. This set of constraints makes up a physical configuration in which the binomial distribution will present itself.