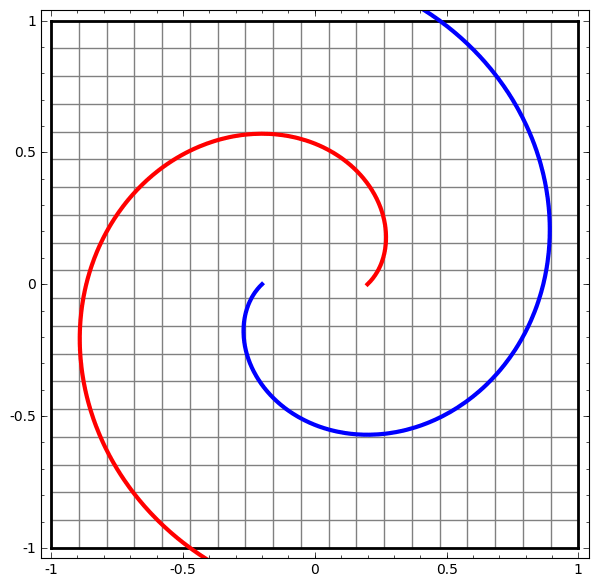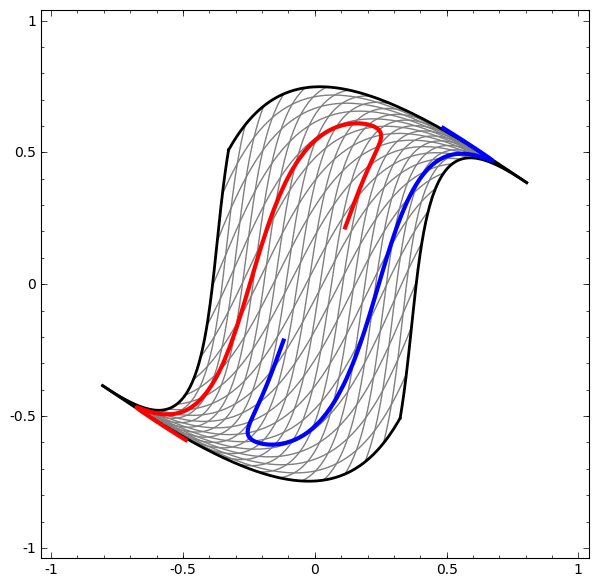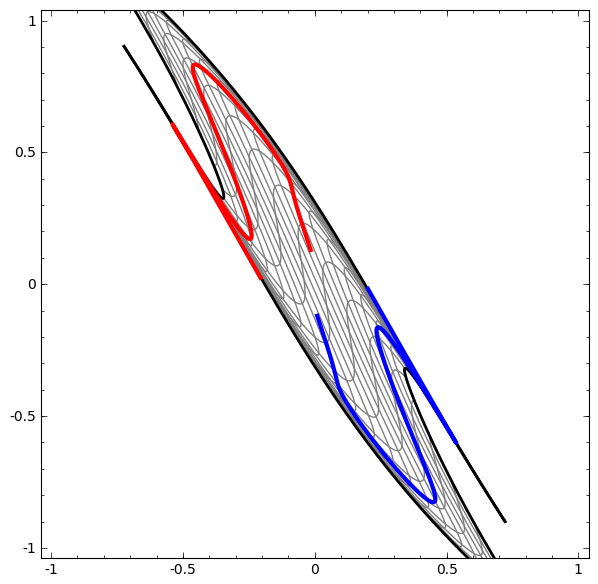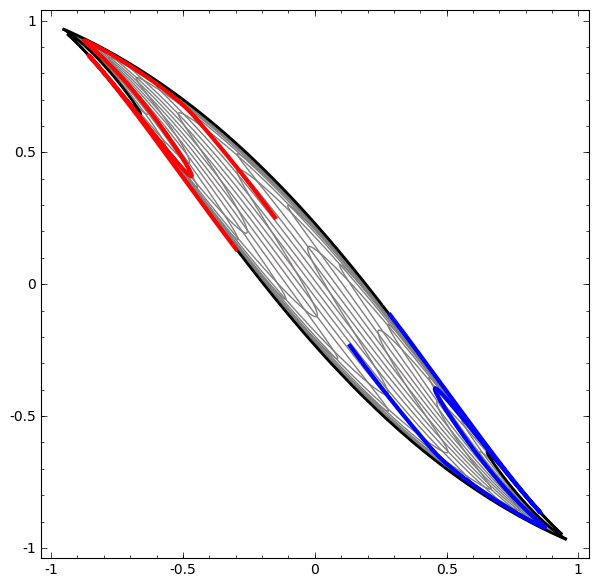
# Purposefully linear, purposefully not linear It is interesting that Deep nets can be thought of a succession of linear transformations, where between each linear transformation a nonlinear activation function is applied (such as Sigmoid or Relu). The result is a transformation such as:  The question is: It seems interesting that we purposefully use a succession of linear transformations, but oddly decide to make them slightly non linear via the use of an activation function. Why is that? JW Answer > Actual linear means that it is going to be reducible. This means you will not be able to build up complexity of topology. So you can't actually build non trivial shapes out of linear (this is a general rule). Linear systems always collapse in boring ways. The math lends itself to be very readily solved. > If things are too nonlinear then you just have pure chaos. You don't have a smooth manifold to move across. > Near linear gives you the reduction preferences that you get from linear systems, but you pin down at a fixed point attractors. You get this cliff where it can't reduce through the nonlinearity and that itself is an information bottleneck in the system. > Compiling a system is saying "go and find all of the non trivial topologies". > This is why ReLU is so nice. It lets you just pinpoint the right spot to put the "crack" that then is a topology changing operator. --- Date: 20211024 Links to: [Linearity](Linearity.md) [003-Data-Science-MOC](003-Data-Science-MOC.md) Tags: #review References: * [Fantastic post from colah's blog on manifolds and topology](https://colah.github.io/posts/2014-03-NN-Manifolds-Topology/)